Abstract
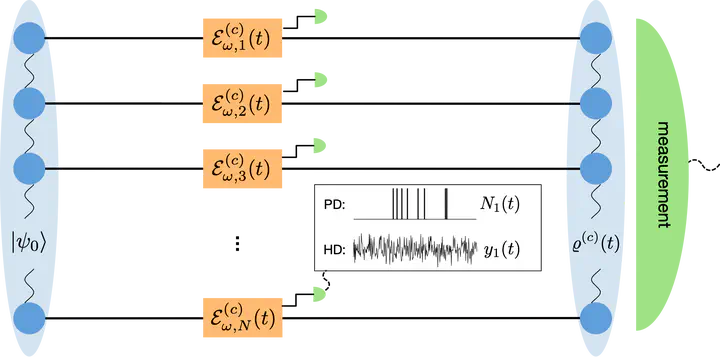
We study quantum frequency estimation for $N$ qubits subjected to independent Markovian noise, via strategies based on time-continuous monitoring of the environment. Both physical intuition and an extended convexity property of the quantum Fisher information (QFI) suggest that these strategies are more effective than the standard ones based on the measurement of the unconditional state after the noisy evolution. Here we focus on initial GHZ states and on parallel or transverse noise. For parallel noise, i.e. dephasing, we show that perfectly efficient time-continuous photo-detection allows to recover the unitary (noiseless) QFI, and thus to obtain a Heisenberg scaling for every value of the monitoring time. For finite detection efficiency, one falls back to the noisy standard quantum limit scaling, but with a constant enhancement due to an effective reduced dephasing. Also in the transverse noise case we obtain that the Heisenberg scaling is recovered for perfectly efficient detectors, and we find that both homodyne and photo-detection based strategies are optimal. For finite detectors efficiency, our numerical simulations show that, as expected, an enhancement can be observed, but we cannot give any conclusive statement regarding the scaling. We finally describe in detail the stable and compact numerical algorithm that we have developed in order to evaluate the precision of such time-continuous estimation strategies, and that may find application in other quantum metrology schemes.