Abstract
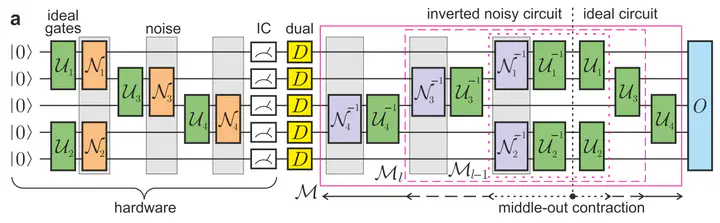
Until fault-tolerance becomes implementable at scale, quantum computing will heavily rely on noise mitigation techniques. While methods such as zero noise extrapolation with probabilistic error amplification (ZNE-PEA) and probabilistic error cancellation (PEC) have been successfully tested on hardware recently, their scalability to larger circuits may be limited. Here, we introduce the tensor-network error mitigation (TEM) algorithm, which acts in post-processing to correct the noise-induced errors in estimations of physical observables. The method consists of the construction of a tensor network representing the inverse of the global noise channel affecting the state of the quantum processor, and the consequent application of the map to informationally complete measurement outcomes obtained from the noisy state. TEM does therefore not require additional quantum operations other than the implementation of informationally complete POVMs, which can be achieved through randomised local measurements. The key advantage of TEM is that the measurement overhead is quadratically smaller than in PEC. We test TEM extensively in numerical simulations in different regimes. We find that TEM can be applied to circuits of twice the depth compared to what is achievable with PEC under realistic conditions with sparse Pauli-Lindblad noise, such as those in [E. van den Berg et al., Nat. Phys. (2023)]. By using Clifford circuits, we explore the capabilities of the method in wider and deeper circuits with lower noise levels. We find that in the case of 100 qubits and depth 100, both PEC and ZNE fail to produce accurate results by using 10^5 shots, while TEM succeeds.