Learning to Measure: Adaptive Informationally Complete Generalized Measurements for Quantum Algorithms
Abstract
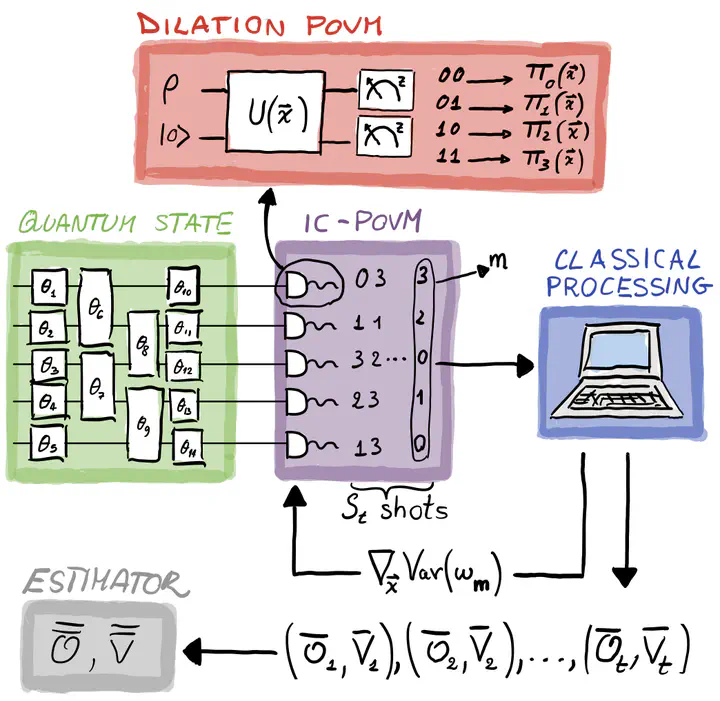
Many prominent quantum computing algorithms with applications in fields such as chemistry and materials science require a large number of measurements, which represents an important roadblock for future real-world use cases. We introduce a novel approach to tackle this problem through an adaptive measurement scheme. We present an algorithm that optimizes informationally complete positive operator-valued measurements (POVMs) on the fly in order to minimize the statistical fluctuations in the estimation of relevant cost functions. We show its advantage by improving the efficiency of the variational quantum eigensolver in calculating ground-state energies of molecular Hamiltonians with extensive numerical simulations. Our results indicate that the proposed method is competitive with state-of-the-art measurement-reduction approaches in terms of efficiency. In addition, the informational completeness of the approach offers a crucial advantage, as the measurement data can be reused to infer other quantities of interest. We demonstrate the feasibility of this prospect by reusing ground-state energy-estimation data to perform high-fidelity reduced state tomography.